torus.cpp
Luis Diaz / July 2023 (9460 Words, 53 Minutes)

Cuando estaba aprendiendo a programar me topé con donut.c, un programa escrito en C por Andy Sloane. Su objetivo era renderizar una dona girando aleatoriamente en el espacio en la terminal usando C ofuscado, incluso su código tiene forma de dona:
k;double sin()
,cos();main(){float A=
0,B=0,i,j,z[1760];char b[
1760];printf("\x1b[2J");for(;;
){memset(b,32,1760);memset(z,0,7040)
;for(j=0;6.28>j;j+=0.07)for(i=0;6.28
>i;i+=0.02){float c=sin(i),d=cos(j),e=
sin(A),f=sin(j),g=cos(A),h=d+2,D=1/(c*
h*e+f*g+5),l=cos (i),m=cos(B),n=s\
in(B),t=c*h*g-f* e;int x=40+30*D*
(l*h*m-t*n),y= 12+15*D*(l*h*n
+t*m),o=x+80*y, N=8*((f*e-c*d*g
)*m-c*d*e-f*g-l *d*n);if(22>y&&
y>0&&x>0&&80>x&&D>z[o]){z[o]=D;;;b[o]=
".,-~:;=!*#$@"[N>0?N:0];}}/*#****!!-*/
printf("\x1b[H");for(k=0;1761>k;k++)
putchar(k%80?b[k]:10);A+=0.04;B+=
0.02;}}/*****####*******!!=;:~
~::==!!!**********!!!==::-
.,~~;;;========;;;:~-.
..,--------,*/
donut.c tiene un lugar especial en mi corazón por el momento en que me topé con él, en su momento se sentía como magia. Ahora que ha pasado el tiempo y sé mucho más que antes, quiero escribir este artículo como la explicación que me habría gustado tener cuando lo vi por primera vez.
Una propiedad interesante de donut.c es que representa la versión mínima viable del pipeline de computación gráfica, se implementa sobre una versión reducida de las bases que usamos para implementar un render. Y lo mejor de todo es que se puede implementar usando un único archivo, sin necesidad de dependencias adicionales más allá de la librería de matemáticas de C.
En este artículo implementaremos paso a paso una versión más legible de donut.c, esta vez en C++. Siguiendo el espíritu de donut.c, tendremos los siguientes objetivos:
- El código debe ser un sólo archivo,
torus.cpp - El código debe ser lo más sencillo posible, trataremos de usar solo funciones y estructuras de control básicas.
- No importaremos nada adicional, más allá de algunas librerías de C++ para imprimir, tomar el tiempo, y hacer cálculos matemáticos.
- Por fines didácticos, nuestro programa estará más enfocado en la legibilidad que en la ofuscasión, a diferencia del programa de Sloane.
- Finalmente, ¡vamos a dibujar una dona (torus o toroide) rotando en la terminal!
Dibujando en la terminal
La idea es crear un programa que se ejecute infinitamente reemplazando una matriz de caracteres de tamaño $R$ en la terminal con una pequeña variación de sí misma. Sin embargo, usualmente la terminal está destinada a imprimir texto de forma continua, dejando registro del texto que se ha impreso hasta ahora, a diferencia de las ventanas donde se dibuja una interfaz gráfica que se actualiza en cada iteración del programa. Por esta razón, lo primero que debemos hacer es buscar una forma de actualizar un conjunto de celdas en una terminal en lugar de empilarlas continuamente. Esto varía un poco según el emulador de terminal que uses, pero sigue más o menos el mismo patrón en todos: Códigos de escape ANSI.
Los códigos de escape ANSI se usan para indicarle algún comportamiento en particular a la terminal, como imprimir los caracteres en cierto color o tipo de fuente, o cambiar la posición del cursor, que es el caso que nos interesa ahora mismo
Usaremos códigos ANSI para indicarle al emulador de terminal que mueva el cursor, que es la barra blanca que marca el la posición del siguiente caracter a introducir. Usualmente siempre está al final del texto más reciente, pero usando códigos de escape ANSI podemos indicarle que se mueva a la posición que necesitemos.
Para saber más sobre códigos de escape ANSI, en este artículo puedes conseguir una buena explicación al respecto. Por ahora solo nos interesa saber que el código que necesitamos tiene la siguiente forma \033[<un_numero>A , donde:
\033[indica que estamos llamando a una funciónAes el nombre de la función, que en este caso significa “mover cursor una cantidad de filas hacia arriba”<un_numero>es el argumento de la función, que en este caso representa la cantidad de líneas que queremos saltar.
Ahora, ¿cómo podemos utilizar esto? Queremos imprimir y reemplazar una matriz de tamaño $R \times R$, esto podemos hacerlo con el siguiente loop:
// Imprime continuamente cada vez que puedas
while(true)
{
for(int i = 0; i < R; i++)
{
for(int j = 0; j < R; j++)
{
cout << "#"; // Imprime los caracteres de esta línea
// En algunas terminales puede haber más espacio entre filas que entre
// columnas de texto, para estos casos podemos añadir un espacio en blanco
// en forma de padding entre columnas.
// cout << " ";
}
cout << endl; // Imprime el salto de línea que marca el final de la línea
}
// Esto es necesario para forzar a la terminal a imprimir lo que tiene en buffer
cout << flush;
}
Consideremos este ciclo, al final del doble ciclo for habremos impreso R filas en la terminal, y el cursor estará en la fila R+1, porque la última fila también incluye un salto de línea. Más aun, estará al inicio de la fila R+1, por lo que para volver a la posición original, solo necesitamos mover el cursor R filas hacia arriba, imprimiendo el código \033[RA con cout :
while(true)
{
// ... doble for
cout << flush;
cout << "\033[" << R << "A";
}
Podemos visualizar esto más fácilmente con un ejemplo:
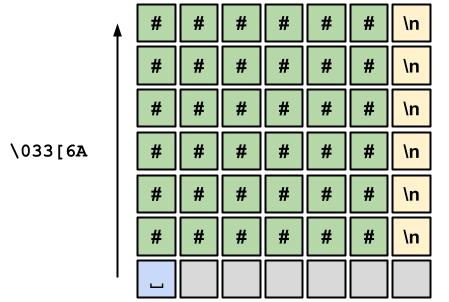
Ahora que definimos un área consistente donde dibujar, aun nos faltan dos cosas para empezar a trabajar en el renderizado:
- Un intervalo de tiempo: Ahora mismo nuestro programa está dibujando cada vez que puede, pero esto puede ser muy intensivo para el procesador y nos gustaría indicar un límite de “fotogramas” por segundo. Además, necesitaremos el tiempo transcurrido para operaciones que dependan del tiempo, como la rotación.
- Donde almacenar el dibujo: Como queremos dibujar un valor distinto por pixel, entonces necesitamos una matriz donde guardar estos datos para mandarlos a dibujar
Intervalo de tiempo
Ahora necesitamos indicarle al programa qué tan seguido deseamos que se ejecute el programa. Para esto mandaremos a nuestro programa a dormir por una cantidad de tiempo al final de cada iteración. Para esto necesitamos incluir thread y chrono . El primero nos da acceso a la función que usaremos para poner a dormir nuestro thread, y el segundo nos permite trabajar con intervalos de tiempo. Esto lo podemos hacer añadiendo los siguientes includes al inicio de nuestro programa:
#include <chrono>
#include <thread>
Para poner a dormir el hilo actual, (el main thread) usaremos la siguiente línea:
this_thread::sleep_for(chrono::milliseconds(30));
this_thread::sleep_for(X)se usa para poner al main thread a dormir por una cantidad especificada de tiempochrono::milliseconds(X)representa un intervalo de X milisegundos- Escogemos 30 milisegundos para alcanzar la marca de 30 FPS, lo que significa que cada iteración debería durar aproximadamente 0.030 (1/30) segundos o 30 milisegundos. Para simplificar este programa asumiremos que el main loop siempre es instantáneo.
- Esta línea se añade al final del main loop para garantizar que el programa espere un poco luego de haber impreso el fotograma actual
Más adelante necesitaremos una forma de saber cuanto tiempo ha pasado desde el inicio de la aplicación para poder hacer operaciones que dependan del tiempo.Por esta razón, usaremos una variable que indique el tiempo que ha transcurrido desde el inicio.
// Main loop
auto frame_start = chrono::high_resolution_clock::now();
float time_passed = 0;
while (true)
{
// Calcula la diferencia de tiempo entre el frame anterior y el frame actual,
// y se añade a la variable acumuladora time_pass
auto now = chrono::high_resolution_clock::now();
auto delta_time = chrono::duration_cast<chrono::milliseconds>(now - frame_start).count() / 1000.0f;
time_passed += delta_time;
frame_start = now;
// ... el resto del main loop
}
frame_startes un objeto que representa un momento en el tiempo. En particular, representa el inicio del frame que está actualmente en curso siendo procesado.time_passedes la cantidad de tiempo que ha transcurrido desde el inicio del programa en segundos- Cuando se inicia el ciclo, guardamos en
nowel momento en que entramos en el ciclo, y luego calculamos la diferencia de tiempo que hubo entrenowy la última vez que se inició el ciclo,frame_start. Esta diferencia se la sumamos al acumulador del tiempo que ha pasado,time_passed. - La línea
chrono::duration_cast<chrono::milliseconds>(now - frame_start).count() / 1000.0f;simplemente está contando la cantidad de milisegundos que hay entrenowyframe_start, y convirtiendolo a segundos.
De esta forma ahora tendremos la cantidad de tiempo que ha pasado desde el inicio del programa en time_passed y al final de cada iteración nuestro programa esperará un poco para el siguiente fotograma.
Canvas
Ahora mismo estamos imprimiendo el mismo caracter continuamente en la terminal, pero queremos que el caracter dependa de la posición en el área donde estamos dibujando. Para esto usaremos una matriz de caracteres de tamaño $R \times R$ donde vamos a almacenar los caracteres que vamos a dibujar en la terminal. Simplemente crearemos una matriz char canvas[R][R] que usaremos para dibujar en la terminal:
while(true)
{
// ... Calculamos el tiempo ...
for (int i = 0; i < R; i++)
for (int j = 0; j < R; j++)
cout << canvas[i][j] << " ";
// ... Resto del main loop ...
}
El espacio adicional que se imprime luego del caracter no es necesario, pero personalmente me gusta añadirlo para darle un acabado más limpio a la imagen resultante. Si pruebas el programa tal como está hasta ahora, es posible que veas una matriz de caracteres sin sentido. Esto es normal, y se debe a que, dependiendo de donde hayas declarado la matriz canvas , es posible que su memoria esté sin inicializar. También puedes añadir una función para limpiar el canvas antes de iniciar, pero de todas formas haremos esto más adelante cuando actualicemos el canvas.
Hasta ahora, deberías tener las siguientes funcionalidades implementadas:
- Se puede imprimir en terminal reemplazando la imagen anterior en lugar de llenando la terminal con muchas repeticiones de la misma imagen
- Existe un intervalo de tiempo entre cada fotograma: las iteraciones del main loop no se ejecutan de inmediato
- Tenemos una variable que contiene el tiempo que ha transcurrido desde el inicio del programa y se actualiza en cada iteración.
- El contenido de los pixeles se guarda en una matriz de tamaño $R$, la resolución escogida, y se imprime desde esta matriz.
Confirma que todo ha ido bien hasta el momento antes de continuar, y empezaremos a trabajar en el dibujo de nuestra dona.
Actualización del canvas
Para actualizar el canvas, nuestra primera intuición podría ser iterar pixel por pixel de la matriz de caracteres asignando un caracter a cada uno dependiendo de su posición. Este enfoque sería el que usaríamos usando Ray Tracing, pero podemos hacerlo de una forma más sencilla.
Aprovechándonos de la poca resolución de la terminal, nuestra solución será una simplificación del pipeline de computación gráfica. La idea será la siguiente:
- Crearemos todos los puntos del torus, como los de un modelo 3D.
- Por cada punto, lo transformaremos para que el objeto sea visibile y tenga el aspecto que deseamos en nuestro canvas. Esta etapa corresponde al Vertex Shader en el pipeline de computación gráfica
- Luego de transformarlo, buscaremos el pixel donde cae este punto, o mejor dicho su posición en la matriz de canvas. Este paso corresponde al rasterizado, pero simplificado para adaptarlo a la poca resolución de la terminal.
- Luego, usando la dirección de la luz y la normal en ese punto, escogeremos el caracter que asignaremos a esa posición de la matriz, coloreando este pixel. Este paso es correspondiente al shading o Fragment Shader.
Antes de empezar, configuraremos la función donde vamos a trabajar. La función update_canvas se encargará de actualizar el canvas de caracteres en cada iteración del main loop. Como nuestro canvas debe ser accesible para el main, entonces pasaremos esta matriz por referencia a la función de update. Así, la versión inicial queda:
void update_canvas(char (&canvas)[R][R])
{
// TODO: Actualizar canvas
}
El tipo del parámetro
canvaspuede verse un poco extraño, pero los paréntesis simplemente indican que el parámetro es una matriz de caracteres pasada por referencia, en lugar de un arreglo de referencias a caracteres, lo cual generaría un error de compilación. Es importante pasar este arreglo por referencia porque de lo contrario, el contenido completo del arreglo se copiaría en los argumentos de la función y este puede ser grande. Además el arreglo externo no se modificaría, por lo que se tendría que devolver el arreglo resultante por valor, lo cual implicaría otra copia.
Añadiremos esta función a nuestro main loop, justo antes de imprimir los caracteres en la terminal.
while(true)
{
// ... Calculamos el tiempo ...
update_canvas(canvas);
for (int i = 0; i < R; i++)
for (int j = 0; j < R; j++)
cout << canvas[i][j] << " ";
// ... Resto del main loop ...
}
Ahora que nuestra función update_canvas está en su lugar, podemos empezar a implementarla.
Generando vértices
Antes de empezar, limpiaremos el canvas asignando el caracter en blanco ' ' a cada casilla, de tal forma que esté “en blanco”, esto se debe a que solo asignaremos el color de una casilla si esta corresponde a un punto del toroide.
void update_canvas(char (&canvas)[R][R])
{
// Limpiamos el canvas asignando un
// caracter en blanco a cada posición
for(int i = 0; i < R; i++)
for(int j = 0; j < R; j++)
canvas[i][j] = ' ';
}
El siguiente paso consiste en generar los puntos del torus. Normalmente cargaríamos un modelo desde un archivo, pero el torus es una figura paramétrica, así que podemos usar una función para generar los vértices. Usaremos la siguiente función:
\[P(\theta, \phi) = \begin{cases} (r_a + r_bcos(\theta)) cos(\phi)\\ (r_a + r_bcos(\theta)) sin(\phi)\\ -r_b\ cos(\theta) \end{cases} \\ \\ 0\le \theta \le 2 \pi \\ 0\le \phi \le 2 \pi \\\]Donde:
- $\color{red}{r_a}$ es el radio de la circunferencia del torus
- $\color{blue}{r_b}$ es el radio del “tubo”, el círculo que se rota para conseguir el torus, que es un sólido en revolución.
- $\color{blue}\theta, \color{red}\phi$ son ángulos que se usan para parametrizar la figura del torus. El ángulo $ \color{blue} \theta$ indica en qué parte de la circunferencia externa estamos, mientras que el ángulo $ \color{red} \phi$ indica la posición en la circunferencia interna.
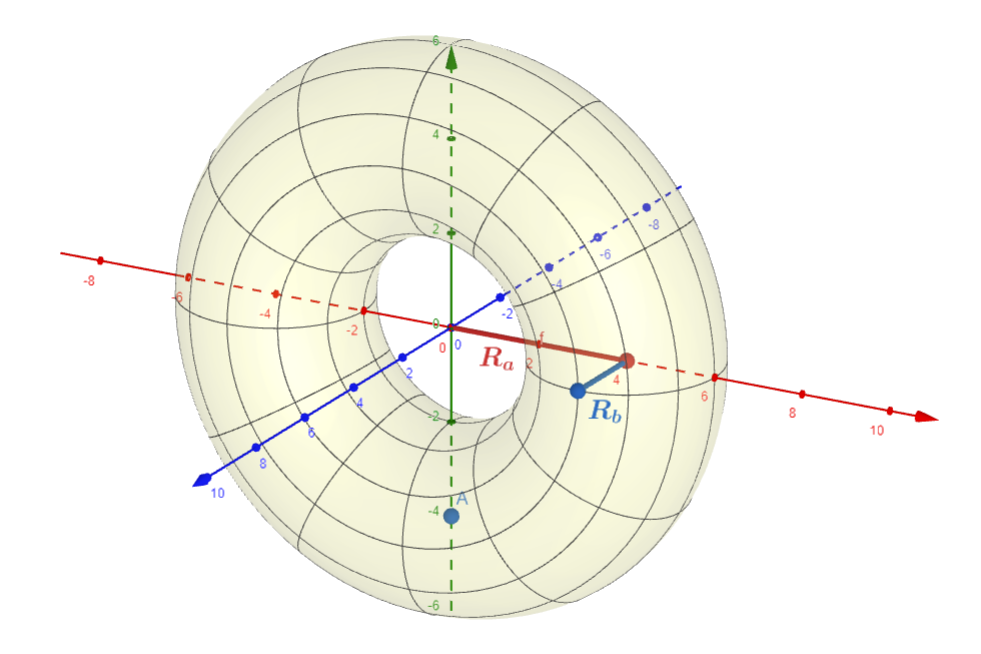
Los parámetros $\color{red}{R_a}$, $\color{blue}{R_b}$, corresponden a los radios del círculo y el tubo respectivamente, los ejes son $\color{red}X$, $\color{green}Y$, $\color{blue} Z$
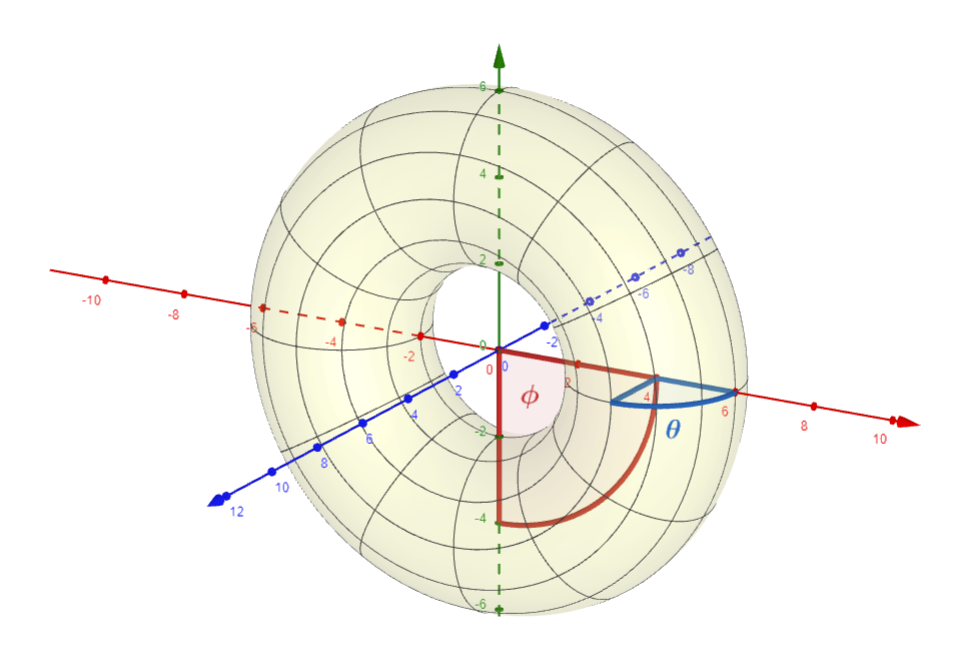
El ángulo $\color{blue}\theta$ corresponde al ángulo en la circunferencia del tubo, y el ángulo $\color{red}\phi$ corresponde al ángulo en la circunferencia interna.
Para representar esta ecuación paramétrica del toroide, usaremos la siguiente función:
void torus_point(float theta, float phi, float torus_radius, float tube_radius, float &out_x, float &out_y, float &out_z)
{
out_x = (torus_radius + tube_radius * cos(theta)) * cos(phi);
out_y = (torus_radius + tube_radius * cos(theta)) * sin(phi);
out_z = -tube_radius * sin(theta);
}
Para usar las funciones cos y sin vamos a necesitar incluir math, con #include <math>.
Esta función simplemente calcula las tres coordenadas de un punto del torus usando la ecuación que mostramos hace un momento. Notemos que, como devolveremos tres valores, se pasan por referencia las variables donde se almacenan los resultados. Como ejercicio adicional, podría implementar un struct que represente un punto o vector. En este artículo no lo haremos para limitarnos a usar solo variables, funciones y estructuras de control básicas.
El toroide es una superficie continua, lo que significa que tiene infinitos puntos, pero nosotros necesitamos solo algunos.
Como tenemos dos valores que parametrizan los puntos en el toroide, $\color{blue} \theta, \color{red} \phi$, entonces para obtener los vértices necesitamos una secuencia de pares de valores para $\color{blue} \theta, \color{red} \phi$. Para escoger estos pares, tal como iteraríamos en una matriz, iteraremos sobre los anillos y vértices por anillo del toroide.
Para saber cuantos pares de valores generaremos, debemos escoger una resolución. La resolución nos indica cuantos anillos y vértices por anillos tendremos. Mientras más alta sea la resolución del modelo, mayor calidad tendrá el modelo resultante, pero también ocupará más memoria y tiempo de procesamiento. En nuestro caso, como la terminal tiene muy poca resolución, no necesitamos un modelo muy detallado. Por simplicidad, usaremos la misma resolución para la cantidad de anillos y vértices.
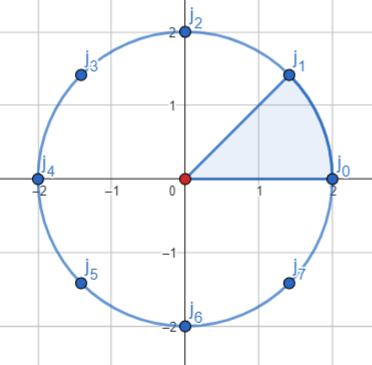
Este es un uno de los anillos del toroide, se puede ver como un corte en el tubo. Cada punto corresponde a un vértice en la superficie del toroide. Como la resolución es 8, tenemos 8 vértices por anillo.
Notemos que como $0 \le {\color{blue}\theta}, {\color{red}\phi} \le 2 \pi$, entonces el ángulo entre cada par de puntos es $2\pi / resolución$.
Finalmente, podemos calcular los puntos con la siguiente función:
void update_canvas(char (&canvas)[R][R])
{
// ... Limpiamos el canvas ...
const int TORUS_RESOLUTION = 200; // Escogemos una resolución
// El ángulo entre cada par de anillos o puntos. M_PI viene incluido
// en math
const float step_size = (2.f * M_PI) / TORUS_RESOLUTION;
// Calcula los radios del toroide. En este caso, usaré la resolución del canvas
// para calcular el tamaño del toroide.
const float tube_radius = ((float) R) / 4.f;
const float torus_radius = ((float) R) / 2.f;
for (int i = 0; i < TORUS_RESOLUTION; i++)
{
const float phi = step_size * i;
for (int j = 0; j < TORUS_RESOLUTION; j++)
{
const float theta = step_size * j;
float x, y, z; // coordenadas del punto
torus_point(theta, phi,torus_radius, tube_radius, x, y, z);
}
}
}
Como mencionamos al principio, usaremos un enfoque orientado a vértices, así que iteraremos por los vértices del modelo en lugar de los pixeles de la imagen. Por esta razón, la mayoría del trabajo que haremos a continuación será en el for loop que acabamos de crear.
En este momento estamos en capacidad de actualizar el canvas y de generar los puntos del toroide, sin embargo seguimos sin ver nada en la terminal. Para resolver esto, añadiremos algo de código temporal que nos permitirá tener mejor feedback de nuestro trabajo.
void update_canvas(char (&canvas)[R][R])
{
// ... Limpiamos el canvas ...
// ... Escogemos los radios del torus y su resolución ...
for (int i = 0; i < TORUS_RESOLUTION; i++)
{
const float phi = step_size * i;
for (int j = 0; j < TORUS_RESOLUTION; j++)
{
const float theta = step_size * j;
// ... Calculamos la posición x,y,z del vértice actual ...
int x_int, y_int;
x_int = (int) x;
y_int = (int) y;
if (0 <= x_int && x_int < R && 0 <= y_int && y_int < R)
{
canvas[y_int][x_int] = '#';
}
}
}
}
- Con este programa, estamos asignando el pixel como
#en caso de que contenga un vértice. - Contraintuitivamente, la coordenada X se corresponde al segundo índice de la matriz. Esto se debe a que ese índice es el que avanza las posiciones en la matriz horizontalmente. Análogamente, la coordenada Y corresponde al primer índice en la matriz.
- Esencialmente estamos usando proyección ortográfica , puesto que el objeto que veamos no considerará profundidad.
- Más adelante modificaremos esta función para incluir un coloreado más apropiado y proyección en perspectiva, pero por ahora esto nos servirá para probar.
- En este programa también podemos ver la relación entre las coordenadas del canvas y el del toroide.
En la siguiente imagen se ilustrala relación entre el canvas y la geometría del toroide. La posición [0][0] de la matriz corresponde a los puntos en el intervalo $[0,1)\times[0,1)$, la casilla [0][1] a los puntos en $[0,1)\times[1,2)$, y así sucesibamente. Es decir, el canvas es una ventana que va desde el origen hasta el punto $(R,R)$.
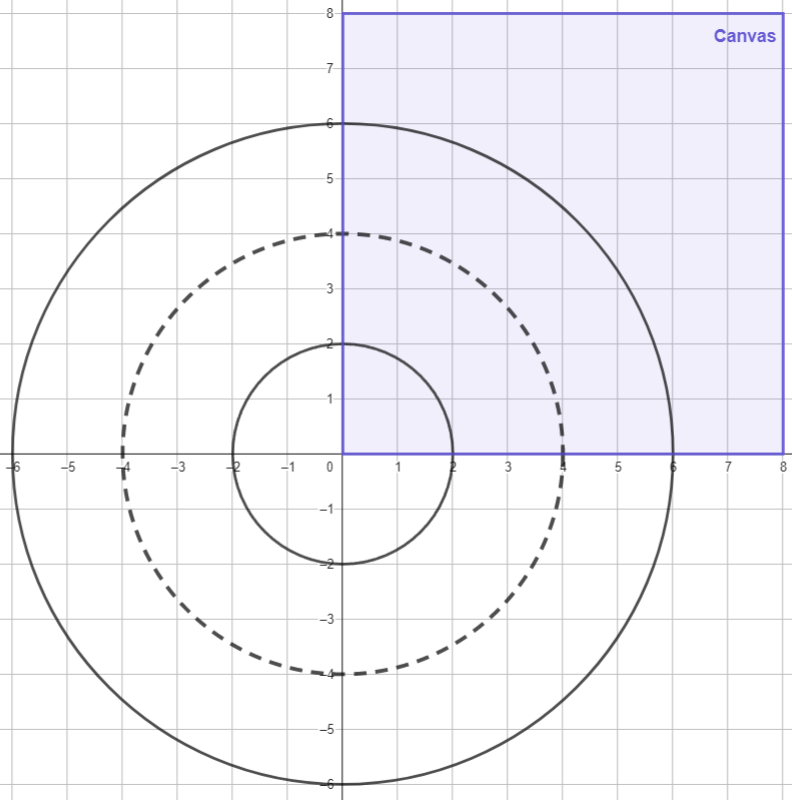
Notemos que el eje Y está reflejado hacia abajo en nuestor canvas, dado que los índices de las filas aumentan hacia abajo, mientras que en el plano cartesiano aumentan hacia arriba. Es decir, el eje Y positivo apunta hacia abajo, tal como en Godot. Por esta razón, la imagen que verás para este momento será el arco de toroide en el primer cuadrante del plano, pero reflejado respecto al eje X.
Transformando vértices
Ahora, aunque estemos en capacidad de visualizar el toroide en la terminal, es posible que no podamos verlo completo o que esté mal ubicado en la imagen. Por esta razón, a continuación añadiremos funciones de transformación para poder visualizar el toroide.
Añadiremos las siguiente función de traslación:
void translate(float offset_x, float offset_y, float offset_z, float x, float y, float z, float& out_x, float& out_y, float& out_z)
{
out_x = x + offset_x;
out_y = y + offset_y;
out_z = z + offset_z;
}
Esta función simplemente toma las coordenadas originales y le suma un desplazamiento. Podemos usarla para desplazar los puntos del toroide en el canvas.
También añadiremos la función de escalado, puesto que es posible que el toroide sea demasiado grande para ser visible en el canvas:
void scale(float scale, float x, float y, float z, float& out_x, float& out_y, float& out_z)
{
out_x = scale * x;
out_y = scale * y;
out_z = scale * z;
}
La función de escalado es útil para fines de pruebas, pero más adelante usaremos la proyección en perspectiva para escalar el toroide modificando su distancia a la cámara. Por ahora, escalar nos sirve para visualizar el toroide.
Con el siguiente código justo después de crear los puntos del toroide podremos centrar el toroide en nuestro canvas:
// Update Canvas:
// ... Limpiamos el canvas ...
// ... Escogemos los radios del torus y su resolución ...
for (int i = 0; i < TORUS_RESOLUTION; i++)
{
const float phi = step_size * i;
for (int j = 0; j < TORUS_RESOLUTION; j++)
{
const float theta = step_size * j;
// ... Calculamos la posición x,y,z del vértice actual ...
scale(0.5, x,y,z, x,y,z);
translate(R / 2, R / 2, 40, x,y,z, x,y,z);
// ... Asignamos # a la posición en la matriz que contiene este punto ...
}
}
Este es un buen momento para intentar experimentar con el toroide. Trata de cambiar los valores de traslación y escalado para ver cómo se modifica la imagen que ves.
Ahora que podemos ver el toroide, podemos empezar a hacer otras transformaciones y tener feedback inmediato. Tal como en donut.c, nuestro objetivo es tener un toroide rotando, así que ahora implementaremos las rotaciones alrededor de los ejes:
// Rotate a point around the X axis
void rotate_x(float angle, float x, float y, float z, float& out_x, float& out_y, float& out_z)
{
out_x = x;
out_y = y * cos(angle) - z * sin(angle);
out_z = y * sin(angle) + z * cos(angle);
}
// Rotate a point around the Y axis
void rotate_y(float angle, float x, float y, float z, float& out_x, float& out_y, float& out_z)
{
out_x = x * cos(angle) + z * sin(angle);
out_y = y;
out_z = -x * sin(angle) + z * cos(angle);
}
// Rotate a point around the Z axis
void rotate_z(float angle, float x, float y, float z, float& out_x, float& out_y, float& out_z)
{
out_x = x * cos(angle) + y * sin(angle);
out_y = -x * sin(angle) + y * cos(angle);
out_z = z;
}
Todas las transformaciones afines sobre un vector (rotación, traslación, escalado) se pueden expresar como una multiplicación de matrices de una matriz de transformación con un vector. Estas funciones de rotación simplemente implementan la multiplicación de matrices manualmente, y las matrices originales son las matrices de rotación alrededor de los ejes X, Y y Z. Estas matrices son:
](/assets/images/torus-cpp/Untitled%202.png)
Cortesía de Wikipedia, puedes ver más sobre estas matrices de rotación en su correspondiente página
Estas funciones esperan un ángulo como argumento, así que debemos decidir que ángulo usar en cada iteración. Queremos que la diferencia entre ángulos entre cada par de fotogramas sea poca para generar una animación fluida. Aquí es donde usaremos el parámetro time_passed que calculamos al principio.
Ahora mismo la función de actualización de canvas solo recibe como argumento el canvas donde va a dibujar, pero añadiremos un argumento adicional que será el tiempo pasado en segundos desde el inicio del programa:
void update_canvas(char (&canvas)[R][R], float time_passed)
{
// ...Actualización del canvas...
}
Y en el main loop usaremos la variable time_passed que calculamos anteriormente:
// main loop
while(true)
{
// ... Calculo del tiempo ...
update_canvas(canvas, time_passed);
// ... Dibujo del canvas ...
}
Con el parámetro del tiempo transcurrido podremos calcular la rotación del toroide en cada fotograma:
for (int i = 0; i < TORUS_RESOLUTION; i++)
{
const float phi = step_size * i;
for (int j = 0; j < TORUS_RESOLUTION; j++)
{
const float theta = step_size * j;
// ... Calculamos la posición x,y,z del vértice actual ...
rotate_y(time_passed, x,y,z, x,y,z);
rotate_x(time_passed * 1.13, x,y,z, x,y,z);
rotate_z(time_passed * 1.74, x,y,z, x,y,z);
// ... Escalamos y trasladamos los puntos del toroide ...
// ... Asignamos # a la posición en la matriz que contiene este punto ...
}
}
- En este programa, usamos el tiempo transcurrido para calcular el ángulo de rotación alrededor de cada eje.
- Cada llamada a función multiplica el tiempo transcurrido con un escalar distinto para que cada eje tenga una velocidad de rotación distinta.
- Es importante aplicar rotaciones antes de traslaciones, porque las rotaciones de un objeto trasladado rotan el objeto alrededor del origen, no alrededor del eje del objeto. En los objetos que están en el origen, su eje de rotación coincide con el origen.
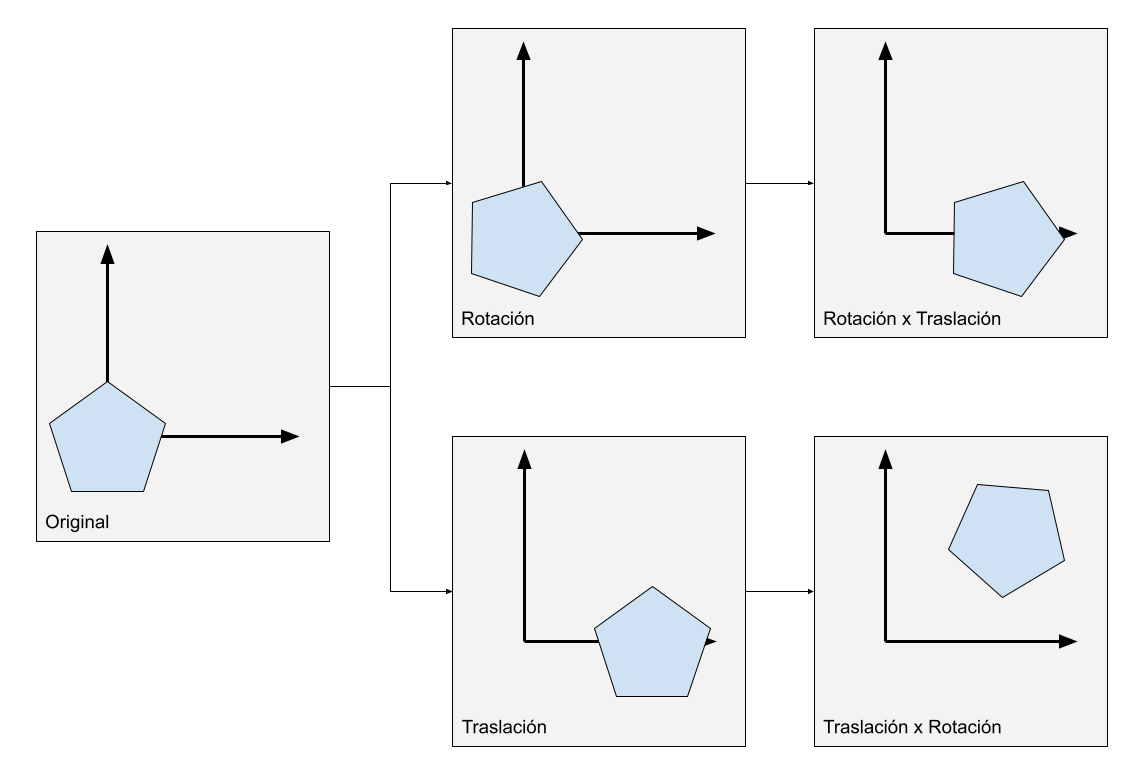
📝 Nota: En realidad es posible rotar después de trasladar, usando la matriz de rotación que también depende del eje de rotación. Las matrices de rotación que estamos usando asumen que el eje de rotación es está en el origen (cada eje del origen dependiendo de la rotación), y nos quedaremos con ellas por simplicidad.
Proyección en perspectiva
Proyectar es el proceso de transformar una representación geométrica en 3D en una en 2D. En nuestro caso, queremos transformar puntos 3D en una imagen 2D. Naturalmente, proyectar se traduce en conseguir una función para transformar puntos 3D en puntos 2D.
Actualmente estamos usando proyección ortográfica. Es decir, convertimos puntos $(x,y,z)$ en puntos $(x’, y’)$ simplemente descartando la coordenada Z:
\[Ortho(x,y,z) = (x,y)\]Este tipo de projección es la que hemos usado hasta ahora. Es simple y nos facilita visualizar los objetos en 3D. Sin embargo no considera la profundidad, así que los objetos que están lejos se ven del mismo tamaño que si estuvieran cerca. Intuitivamente, esto es una consecuencia de ignorar la coordenada Z, nuestra función de proyección está ignorando la profundidad de los puntos.
.png)
Proyección ortográfica: Los puntos del cubo se transforman a puntos en el plano simplemente descartando su coordenada Z.
Ahora buscaremos implementar proyección en perspectiva, es un estilo de proyección que considera la profundidad, para que objetos lejanos se vean más pequeños que objetos cercanos a la cámara. La idea será escalar los puntos $(x,y)$ linealmente respecto a su coordenada $z$. Para esto, consideremos la siguiente imagen:
.png)
La idea es crear un plano virtual que se encuentra a cierta distancia de la cámara y proyectar los puntos de nuestra geometría 3D en esta superficie 2D. El contenido del plano se dibujará al canvas. Para conseguir esta transformación, vamos a considerar el teorema de proporcionalidad de triángulos, o teorema de Thales para determinar la posición $(x’, y’)$ en este plano virtual.
El teorema de Thales nos indica que si intersectamos un triángulo con una recta paralela a uno de sus lados, obtenemos las siguientes relaciones:
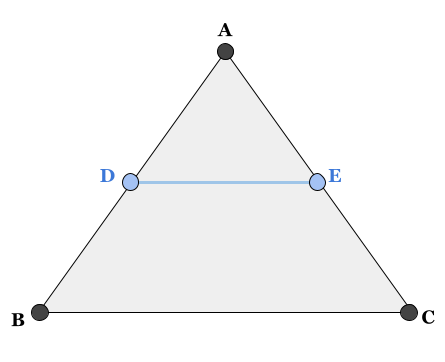
En este ejemplo, la recta $\color{blue}{DE}$ es paralela al lado $BC$, y los puntos de intersección generan estas relaciones. Como veremos más adelante, la más útil será la segunda relación, ya que nos permite relacionar la longitud de la recta intersección $\color{blue}{DE}$ con las longitudes de de los segmentos intersectados por la recta.
Ahora veamos más detalladamente la definición de nuestro plano virtual para identificar donde usar el teorema de Thales:
.png)
En esta imagen estamos viendo una perspectiva lateral de la cámara. Y asumiendo que se encuentra en el origen, podemos identificar los siguientes valores:
- $z’$ Es la distancia desde la cámara hasta el plano virtual, este es un valor que podemos definir manualmente.
- $y’$ es el valor que estamos buscando para la proyección del punto $(x,y,z)$ en el plano virtual.
- $y,z$ son valores reales del punto que queremos proyectar, ambos son valores conocidos.
Usando la parte (b) del teorema de Thales, podemos derivar la siguiente relación:
\[\frac{z}{z'} = \frac{y}{y'}\]Y como solo desconocemos el valor de $y’$, entonces podemos despejarlo de la ecuación:
\[y' = \frac{y z'}{z}\]Análogamente, podemos usar la misma lógica para conseguir el valor de $x’$:
\[x'=\frac{xz'}{z}\]Para conseguir este valor podemos considerar la proyección en el plano $XZ$ en lugar del plano $YZ$ que usamos en la última imagen. Esta proyección corresponde a una vista de arriba hacia abajo de la cámara.
Finalmente, nuestra función de proyección en perspectiva se reduce a:
\[Perspective(x,y,z) = (\frac{xz'}{z}, \frac{yz'}{z})\]Donde:
- Como mencionamos anteriormente, $z’$ es una constante positiva, la distancia de la cámara al plano virtual, y podemos fijarla como nos sea conveniente.
- Como la cámara se encuentra en el origen, entonces mientras mayor sea $z$, entonces más pequeños se vuelven los valores de $x,y$. Es decir, los objetos que se encuentren más alejados de la cámara, se ven más pequeños.
- Como asumimos que la cámara está en el origen, entonces z debe ser positivo para ser visible. Más aun, debe ser mayor a la distancia de la cámara $z’$.
Ahora, llevando nuestra teoría recién adquirida a nuestro programa, volveremos a la función de actualización de canvas, específicamente a la parte donde proyectamos los puntos 3D a puntos 2D:
// Update Canvas:
// ... Limpiamos el canvas ...
// ... Escogemos los radios del torus y su resolución ...
for (int i = 0; i < TORUS_RESOLUTION; i++)
{
const float phi = step_size * i;
for (int j = 0; j < TORUS_RESOLUTION; j++)
{
const float theta = step_size * j;
// ... Calculamos la posición x,y,z del vértice actual ...
// ... Calculamos rotaciones, traslaciones y escalado de este punto ...
int x_int, y_int;
// Reemplazamos la proyección ortográfica....
// x_int = (int) x;
// y_int = (int) y;
// Por la proyección en perspectiva:
x_int = (int) (CAM_DISTANCE_TO_SCREEN * x / z);
y_int = (int) (CAM_DISTANCE_TO_SCREEN * y / z);
if (0 <= x_int && x_int < R && 0 <= y_int && y_int < R)
{
canvas[y_int][x_int] = '#';
}
}
}
CAM_DISTANCE_TO_SCREENEs unfloatconstante que representa $z’$ en nuestra ecuación anterior. Puedes definirla en cualquier parte del programa mientras sea alcanzable para este punto. En mi caso, usaré el valor de 20.0.- Ahora que el tamaño del toroide depende de su distancia de la cámara, podemos eliminar el escalado que usábamos anteriormente, la línea
scale(0.5, x,y,z, x,y,z); - Como ahora usamos una forma distinta de proyectar las imagen en pantalla, las traslaciones que hemos hecho para posicionar el toroide pueden no ser las más apropiadas. Modifica las traslaciones que hemos usado para ubicar el toroide en el centro de la pantalla.
- Ahora que usamos proyección en perspectiva, experimenta alejando el toroide aumentando su traslación en la coordenada Z, verás que ahora su tamaño disminuye mientras más lejos esté en el eje Z.
Ahora que tenemos proyección en perspectiva, las partes más lejanas del toroide deberían verse más pequeñas que las más cercanas a la cámara. Para este punto solo necesitamos colorear el toroide para que cada punto de su superficie tenga un color distinto dependiendo de su ángulo respecto a la luz.
Shading
El shading es simplemente escoger un color por cada pixel de la imagen. Como no usaremos colores reales, sino caracteres ascii, en nuestro caso el problema se reduce a conseguir el caracter correcto para cada “pixel”. Usaremos caracteres más densos segun la “claridad” del color en cada punto. Los caracteres que usaremos, ordenados de menor a mayor claridad, son los siguientes:
.,-~:;=!*#$@
Para definir la claridad de cada punto, usaremos una regla muy simple. Vamos a escoger una dirección de luz, y dependiendo de qué tan opuesta sea la normal en cada punto de la superficie a esta dirección, consideraremos que este punto es más claro.
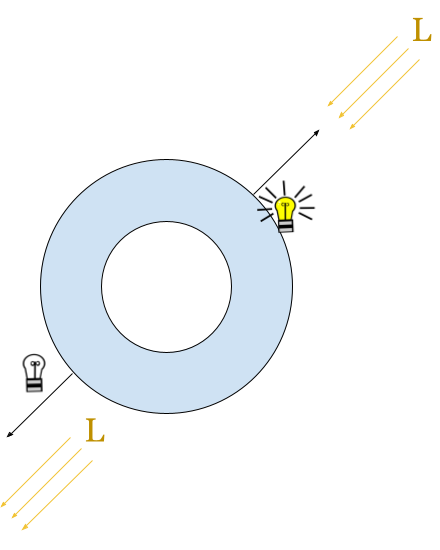
Para esto usaremos el producto interno, entre la dirección de la luz y el vector normal de la superficie. Como sabemos, el producto interno es una función que recibe dos vectores y calcula un valor escalar. Cuando los vectores están normalizados, entonces el escalar está en el rango $[-1,1]$, donde -1 indica que son anti paralelos (son el mismo vector con direcciones opuestas) y 1 indica que son paralelos (son el mismo vector, incluyendo la dirección), y 0 indica que son perpendiculares.
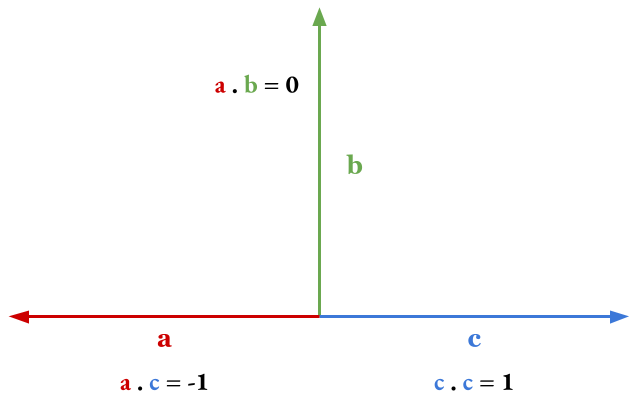
Ejemplos de producto punto. $\color{red}a$ y $\color{green}b$ son perpendiculares, así que su producto punto es 0. $\color{red}a$ y $\color{blue}c$ son antiparalelos, así que su producto punto es -1, y $\color{blue}c$ es paralelo a sí mismo, por lo que el producto consigo mismo es 1. Además, todos los vectores entre $\color{blue}c$ y $\color{green}b$ multiplicados con a producen valores negativos, y todos los vectores entre $\color{blue}c$ y $\color{green}b$ multiplicados con $\color{blue}c$ producen valores positivos.
Ahora que tenemos una idea para colorear nuestros pixeles con caracteres, necesitamos un plan para hacerla realidad. Los pasos son los siguientes:
- Crearemos una función para calcular la normal en cada punto de la superficie del toroide.
- Crearemos una función para calcular el producto punto entre dos vectores
- Añadiremos unas variables para las coordenadas de un vector de dirección de la luz.
- Transformaremos el vector normal para que sea consistente con las transformaciones de nuestro toroide.
- Escogeremos un caracter distinto dependiendo de la magnitud del producto punto entre la dirección de la luz y la dirección de la normal en cada punto
Adicionalmente, un problema que no hemos resuelto hasta ahora es el orden de dibujado. Hasta ahora, estamos dibujando cada punto independientemente de si tiene otro punto más cerca de la cámara. Para esto usaremos z buffering. Crearemos una matriz del mismo tamaño del canvas, que llamaremos z buffer, que tendrá la distancia del punto más cercano dibujado en cada posición del canvas. Si el nuevo punto que vamos a dibujar está más lejos que el punto actual en el z buffer, entonces lo ignoraremos.
Con nuestro plan trazado, procederemos a implementarlo. Empezaremos creando la función para calcular la normal del toroide.
Para empezar, notaremos que el toroide es un sólido en revolución, es una circunferencia trasladada cierta distancia del origen y rotada alrededor de un eje. Sabemos que la normal en un punto de una circunferencia es paralela al vector entre dicho punto y el centro de la circunferencia:
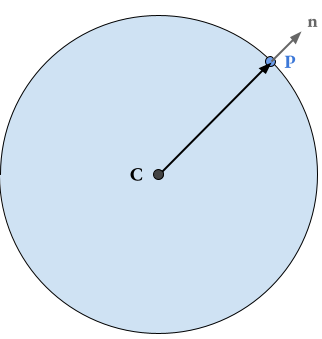
Como vemos en este caso, la circunferencia de centro $C$ tiene normal $\color{gray}{n}$ en el punto $\color{blue} P$, y además $\color{gray}{n}$ es paralelo al vector $C\color{blue} P$. Podemos extrapolar esta misma lógica al toroide notando que cada anillo del toroide es una circunferencia. El punto en la superficie del toroide es un punto de la circunferencia que ya sabemos como calcular, así que solo necesitamos el punto en centro del anillo para calcular el vector normal a la superficie.
Si recordamos la geometría del toroide, notamos que podemos calcular el punto en el centro del tubo como un toroide de radio 0:

En este ejemplo, si hacemos $\color{blue}{R_b} = 0$, entonces el punto obtenido estará siempre en el origen. De esta forma, podemos escribir la siguiente función:
void torus_normal(float theta, float phi, float torus_radius, float tube_radius, float &out_x, float &out_y, float &out_z)
{
float p_x, p_y, p_z;
float c_x, c_y, c_z;
// Calculamos el punto en la superficie
torus_point(theta, phi, torus_radius, tube_radius, p_x, p_y, p_z);
// Calculamos el punto en el centro, es la misma función con un tubo de radio 0
torus_point(theta, phi, torus_radius, 0, c_x, c_y, c_z);
// Calculamos el vector normal como la diferencia entre el centro y el punto
// de superficie:
out_x = p_x - c_x;
out_y = p_y - c_y;
out_z = p_z - c_z;
// Normalizamos el vector normal.
out_x = out_x / tube_radius;
out_y = out_y / tube_radius;
out_z = out_z / tube_radius;
}
- En esta función, calculamos el punto el la superficie usando la función de punto en toroide que definimos anteriormente.
- Luego, usamos esta misma función con radio de tubo 0 para obtener el punto en el centro.
- Calculamos el vector normal como la diferencia entre estos dos vectores.
- Finalmente, como sabemos que la longitud de este vector es igual al radio del tubo, podemos normalizar este vector usando el radio del tubo como magnitud.
Con esta función podremos calcular la normal en cualquier punto de la superficie usando los mismos parámetros que necesitamos para calcular el punto.
Ahora definiremos la función para calcular el producto punto entre dos vectores, esta función es muy simple y es la siguiente:
float dot(float x1, float y1, float z1, float x2, float y2, float z2)
{
return x1 * x2 + y1 * y2 + z1 * z2;
}
A continuación, definiremos las siguientes variables en la función de actualización de canvas para las coordenadas de la dirección de la luz:
float LIGHT_DIR_X = 0, LIGHT_DIR_Y = 1, LIGHT_DIR_Z = 1;
float magnitude = sqrt(LIGHT_DIR_X * LIGHT_DIR_X + LIGHT_DIR_Y * LIGHT_DIR_Y + LIGHT_DIR_Z * LIGHT_DIR_Y);
LIGHT_DIR_X = LIGHT_DIR_X / magnitude;
LIGHT_DIR_Y = LIGHT_DIR_Y / magnitude;
LIGHT_DIR_Z = LIGHT_DIR_Z / magnitude;
Con estas variables definimos la dirección de la luz, está sobre el eje $y$ y apunta hacia abajo y hacia el frente. Notemos que es importante normalizar este vector para que nuestros próximos cálculos sean correctos.
Antes de usar el vector normal, debemos transformarlo para que sea consistente con las transformaciones que hemos aplicado al toroide.
La matemática necesaria para transformar vectores normales se escapa un poco del alcance de este artículo, pero por ahora basta con saber que en este caso solo será necesario aplicar las mismas rotaciones que se aplicaron al punto en el mismo orden:
// Update Canvas:
// ... Limpiamos el canvas ...
// ... Escogemos los radios del torus y su resolución ...
for (int i = 0; i < TORUS_RESOLUTION; i++)
{
const float phi = step_size * i;
for (int j = 0; j < TORUS_RESOLUTION; j++)
{
const float theta = step_size * j;
// ... Calculamos la posición x,y,z del vértice actual ...
// ... Calculamos rotaciones, traslaciones y escalado de este punto ...
float n_x, n_y, n_z;
torus_normal(theta, phi,torus_radius, tube_radius, n_x, n_y, n_z);
rotate_y(time_passed, n_x,n_y,n_z, n_x,n_y,n_z);
rotate_x(time_passed * 1.13, n_x,n_y,n_z, n_x,n_y,n_z);
rotate_z(time_passed * 1.74, n_x,n_y,n_z, n_x,n_y,n_z);
// ... Proyectamos el punto y asignamos # a su posición en el canvas ...
}
}
Finalmente, vamos a asignar el color correcto a cada pixel:
// Update Canvas:
// ... Limpiamos el canvas ...
// ... Escogemos los radios del torus y su resolución ...
for (int i = 0; i < TORUS_RESOLUTION; i++)
{
const float phi = step_size * i;
for (int j = 0; j < TORUS_RESOLUTION; j++)
{
const float theta = step_size * j;
// ... Calculamos la posición x,y,z del vértice actual ...
// ... Calculamos rotaciones, traslaciones y escalado de este punto ...
// ... Transformaciones de la normal ...
// ... Proyectamos el punto y asignamos # a su posición en el canvas ...
if (0 <= x_int && x_int < R && 0 <= y_int && y_int < R)
{
char const SHADES[] = ".,-~:;=!*#$@";
float normal_dot_light = dot(n_x,n_y,n_z, LIGHT_DIR_X, LIGHT_DIR_Y, LIGHT_DIR_Z);
// Sanity check
if (abs(normal_dot_light) >= 1.0f)
normal_dot_light = 1.0f;
// Reemplazamos esta línea ...
// canvas[y_int][x_int] = '#';
// Con esta asignación condicional:
if(normal_dot_light >= 0)
canvas[y_int][x_int] = ' ';
else
canvas[y_int][x_int] = SHADES[(int) (abs(normal_dot_light) * 12)];
}
}
}
- En este código estamos definiendo un arreglo de caracteres ordenados de “menos claro” a “más claro”.
- Calculamos el producto punto entre la normal y la luz
- Nos aseguramos de que el valor del producto punto sea el correcto
- Si el producto punto es mayor o igual que 0, significa que la normal es “paralela” a la luz y por lo tanto es un punto de la superficie que no mira hacia la luz. De lo contrario, está de cara hacia la luz y la refleja con mayor intensidad.
Para este punto es posible que la imagen que veas no tenga los colores correctos, esto se debe a que no estamos revisando si estamos dibujando sobre un pixel que ya es el más cercano a la pantalla. Para esto usaremos el z buffer. Es una matriz del mismo tamaño del canvas donde almacenaremos la componente z del punto correspondiente a cada pixel. Solo dibujaremos puntos si el pixel que le corresponde está vacío o tiene un punto que esté más atrás.
// Update Canvas:
// ... Limpiamos el canvas ...
// ... Escogemos los radios del torus y su resolución ...
float depth_buffer[R][R];
for(int i = 0; i < R; i++)
for(int j = 0; j < R; j++)
depth_buffer[i][j] = 1000000;
// ... Procesamiento de cada punto del toroide ...
- En esta sección estamos creando un z buffer (o depth buffer) del mismo tamaño del canvas
- Lo inicializamos valores lo bastante altos para que cualquier punto esté más adelante que el valor inicial.
Finalmente, para usar el z buffer, simplemente revisamos que el punto actual esté más adelante que el último que haya sido dibujado en la misma posición, y si lo está, actualizamos el z buffer:
// Update Canvas:
// ... Limpiamos el canvas ...
// ... Escogemos los radios del torus y su resolución ...
for (int i = 0; i < TORUS_RESOLUTION; i++)
{
const float phi = step_size * i;
for (int j = 0; j < TORUS_RESOLUTION; j++)
{
const float theta = step_size * j;
// ... Calculamos la posición x,y,z del vértice actual ...
// ... Calculamos rotaciones, traslaciones y escalado de este punto ...
// ... Transformaciones de la normal ...
// ... Proyectamos el punto y asignamos # a su posición en el canvas ...
// Añadimos otro término a la condición del if:
if (0 <= x_int && x_int < R && 0 <= y_int && y_int < R && depth_buffer[y_int][x_int] > z)
{
depth_buffer[y_int][x_int] = z;
// ... Selección del color para este pixel ...
}
}
}
Y con esto hemos terminado nuestro programa. Este fue un viaje largo, pero en el camino aprendimos las bases de computación gráfica, y logramos implementar el renderizado de una figura geométria en 3D usando solo estructuras de control básicas. Con este programa como base es fácil extender la teoría para entender el renderizado con APIs gráficas, como OpenGL.
Con un poco más de trabajo es posible extender este esquema sencillo para hacer estilos de render más complejos. Podrías añadir un parser de modelos 3D para leer los puntos de la superficie junto con sus normales para crear un render de terminal que sirva para cualquier tipo de geometría 3D en lugar de solo con toroides. Yendo un poco más lejos, podríamos mapear colores en RGB a algunos colores en códigos ANSI y usar las UVs para hacer un renderizado sencillo con colores. Incluso podríamos convertirlo en un Ray Tracer recursivo cambiando el enfoque por-punto por un enfoque por-pixel, ¡el cielo es el límite!
El código resultante de este artículo se puede encontrar en el siguiente enlace en GitHub:
GitHub - LDiazN/torus.cpp: A simple torus render in terminal inspired by donut.c
